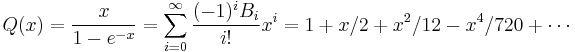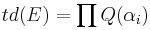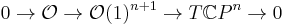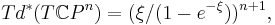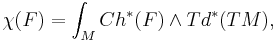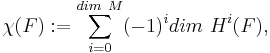Todd class

In mathematics, the Todd class is a certain construction now considered a part of the theory in algebraic topology of characteristic classes. The Todd class of a vector bundle can be defined by means of the theory of Chern classes, and is encountered where Chern classes exist — most notably in differential topology, the theory of complex manifolds and algebraic geometry. In rough terms, a Todd class acts like a reciprocal of a Chern class, or stands in relation to it as a conormal bundle does to a normal bundle.

The Todd class plays a fundamental role in generalising the classical Riemann-Roch theorem to higher dimensions, in the Hirzebruch-Riemann-Roch theorem and Grothendieck-Hirzebruch-Riemann-Roch theorem.

1 History
2 Definition
3 Properties of Todd class
4 Hirzebruch-Riemann-Roch formula
5 See also
6 Notes
7 References

History

It is named for J. A. Todd, who introduced a special case of the concept in algebraic geometry in 1937, before the Chern classes were defined. The geometric idea involved is sometimes called the Todd-Eger class. The general definition in higher dimensions is due to Hirzebruch.

Definition

To define the Todd class td(E) where E is a complex vector bundle on a topological space X, it is usually possible to limit the definition to the case of a Whitney sum of line bundles, by means of a general device of characteristic class theory, the use of Chern roots (aka, the splitting principle). For the definition, let

$Q(x) = \frac{x}{1 - e^{-x}}=\sum_{i=0}^\infty \frac{(-1)^iB_{i}}{i!}x^{i} = 1 %2Bx/2%2Bx^2/12-x^4/720%2B\cdots$

be the formal power series with the property that the coefficient of xⁿ in Q(x)ⁿ⁺¹ is 1 (where the B_i are Bernoulli numbers).

If E has the α_i as its Chern roots, then

$td(E) = \prod Q(\alpha_i)$

which is to be computed in the cohomology ring of X (or in its completion if one wants to consider infinite dimensional manifolds).

The Todd class can be given explicitly as a formal power series in the Chern classes as follows:

td(E) = 1 + c₁/2 + (c₁²+c₂)/12 + c₁c₂/24 + (−c₁⁴ + 4c₁²c₂ + c₁c₃ + 3c₂² − c₄)/720 + ...

where the cohomology classes c_i are the Chern classes of E, and lie in the cohomology group H²ⁱ(X). If X is finite dimensional then most terms vanish and td(E) is a polynomial in the Chern classes.

Properties of Todd class

The Todd class is multiplicative: 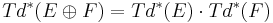$Td^*(E\oplus F) = Td^*(E)\cdot Td^*(F)$

From the Euler exact sequence for the tangent bundle of ${\Bbb C} P^n$

$0 \to {\mathcal O} \to {\mathcal O}(1)^{n%2B1} \to T {\Bbb C} P^n \to 0$

and multiplicativity, one obtains

$Td^*(T {\Bbb C} P^n) = (\xi/(1-e^{-\xi}))^{n%2B1},$

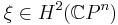where $\xi \in H^2({\Bbb C} P^n)$ is the fundamental class of the hyperplane section.^[1]

Hirzebruch-Riemann-Roch formula

Main article: Hirzebruch–Riemann–Roch theorem

For any coherent sheaf F on a smooth compact complex manifold M, one has

$\chi(F)=\int_M Ch^*(F) \wedge Td^*(TM),$

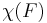where $\chi(F)$ is its holomorphic Euler characteristic,

$\chi(F):= \sum_{i=0}^{dim\ M} (-1)^i dim \ H^i(F),$

and Ch^*(F) its Chern character.

Notes

^ INTERSECTION THEORY CLASS 18, by Ravi Vakil

References

Todd, J. A. (1937), "The Arithmetical Invariants of Algebraic Loci", Proc. London Math. Soc. 43 (1): 190–225, doi:10.1112/plms/s2-43.3.190, Zbl 0017.18504
F. Hirzebruch, Topological methods in algebraic geometry, Springer (1978)
M.I. Voitsekhovskii (2001), "Todd class", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=T/t092930